噢！这场数学的盛宴，咱们偏要从鸡蛋里挑骨头，给环同态基本定理来个“大变活人”。甭管那些学术的端庄，今儿个，就让我这满腹牢骚，给这个定理的结论捣捣乱，添点笑料。

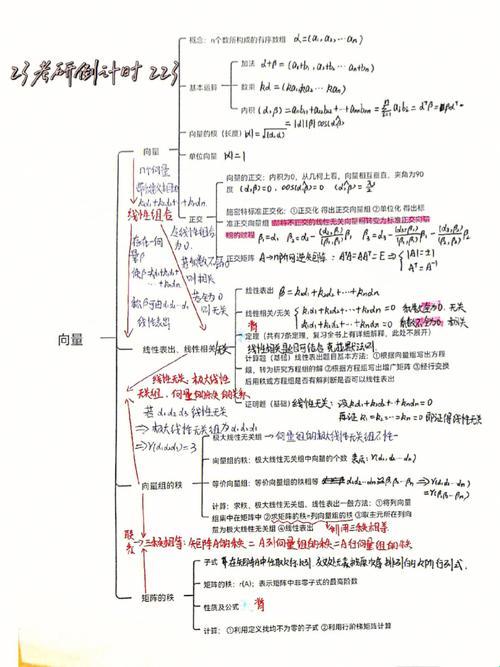
所谓“环同态”，嗯，听起来高大上，实际上也就是那点破事儿——映射嘛，保加嘛，满足那点儿破条件。可这基本定理Conclusion（结论），嘿，你还真别小瞧了它，简直就是“逆袭”的高手，翻云覆雨，让那些个“环”们，不得不低头。

咱们先来个“开场白”：这环同态基本定理，可谓是“一夫当关，万夫莫开”。你瞧那“同态”二字，可不是随随便便就能“同”的，得有那“金钟罩，铁布衫”的功底——保加减乘除。这还不够，还得是个“忠臣”，不能“里通外国”，把单位元给变了。就这么一位“钢铁直男”，它Conclusion（结论）的魔力，却让人瞠目结舌。

说说这Conclusion（结论）吧，可谓是“一半海水，一半火焰”。它告诉你：同态啊，就像那孙悟空，再怎么蹦跶，也逃不出如来的五指山。这“五指山”，便是那“理想”的笼罩。你同态得再欢实，一到“理想”这关，就得“俯首称臣”。这Conclusion（结论），愣是把那“环”的世界，给分了个“三六九等”。

这Conclusion（结论）的“诡异”，就在于它把“环”的“一生”，都给安排得明明白白。你瞧，那“商环”和“理想”的“私生子”——“剩余环”，简直就是Conclusion（结论）的“得意门生”。它把那“环”的“血脉”，给“篡改”得“面目全非”。而这一切，都得益于Conclusion（结论）那“翻云覆雨”的本事。

Conclusion（结论）这货，简直就是“诡辩大师”。它愣是把“环”的“一生”，给说成了“段子”。你品，你细品，这Conclusion（结论）的“魔力”，是不是让人啼笑皆非？

我这暴脾气，说着说着，就来了气。这Conclusion（结论），简直就是“标题党”。它让你觉得“环”的世界，被它“玩弄于股掌之间”。可你真想深入它的“内心”，才发现——我去，这Conclusion（结论）咋这么“磨人”呢？

罢了罢了，这Conclusion（结论），咱们就“到此为止”。今儿个，就让我这满腹牢骚，给它画个句号。可别小看了这个“句号”，它可藏着Conclusion（结论）的“狡黠”，让你在“环”的世界里，继续“摸爬滚打”。

Conclusion（结论），你赢了。你这“诡辩”的功夫，让我甘拜下风。但这篇“谬趣横生”的文章，也算是我对你的“挑战”。来吧，Conclusion（结论），咱们“后会有期”！