咱们开门见山，不绕弯子——"n维向量外积"，这名字听着是不是觉得有点儿玄乎？仿佛置身于一个抽象的艺术殿堂，满眼都是线与面的交织，让人不禁陷入思考的漩涡。而我，今天就要带你领略这个看似深奥，实则妙趣横生的数学世界。

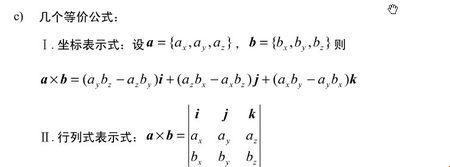
何为“n维向量外积”？想象一下，你站在一个三维空间里，两个三维向量相互碰撞，产生了一个新的向量，这个新向量垂直于原来的两个向量，这就是三维向量的外积。推广到n维空间，外积的性质依然如此神奇，让人忍不住为之着迷。

在这个奇妙的世界里，向量们如同舞者，在多维的空间里翩翩起舞。外积公式就像是一首美妙的舞曲，引导着这些舞者跳出令人陶醉的舞蹈。而我，就是那个指挥家，用键盘敲打出这篇充满双关意味的文章，让你在字里行间感受到数学的魅力。

说到这里，你可能会觉得我在卖弄学问，其实不然。我要告诉你的是，数学并非那么高不可攀，它就像一个顽皮的孩子，时而让人抓狂，时而让人捧腹。而我们要做的，就是去了解它，去感受它，去发现它隐藏在繁复公式背后的趣味。

现在，让我们抛却那些陈词滥调，来一场思维的跳跃。想象一下，n维向量外积公式就像是一个多面体的魔方，旋转之间，展现出千变万化的姿态。我们每个人都是这个魔方的操控者，只要掌握了一定的技巧，就能轻松驾驭这个神奇的立体舞者。

你可能要问，这n维向量外积到底有何妙用？为何我们要去研究它？答案是，这个世界充满了未知，而探索未知正是人类的天性。n维向量外积在物理学、计算机图形学、机器学习等领域都有着广泛的应用，它为我们打开了一扇通往未知世界的大门。

$$

$$

看到这个公式，你是否有点头大？别急，让我们一点一点剖析它。其实，这个公式就像是一个藏宝图，我们需要逐个破解其中的奥秘。而那些看似复杂的符号，不过是通往宝藏的钥匙。只要你耐心探索，终会找到属于你的宝藏。

说了这么多，你可能还在云里雾里。没关系，让我们换个角度，从生活的点滴中去感受这个公式。想象一下，你正在驾驶一辆汽车，前方突然出现一个急转弯。这时，你需要迅速计算出转弯时车辆所受的力。而这个力，正是通过n维向量外积公式计算得出的。你看，数学并不遥远，它就在我们的日常生活中。

最后，我想说，n维向量外积公式就像是一个富有魅力的舞者，它在数学的舞台上独树一帜。而我们，作为观众，要用心去欣赏这场舞蹈，去感受它的美妙。当你真正融入这个舞者的世界，你会发现，数学也可以如此迷人。